2021. 12. 8. 18:44ㆍrequirement fot AI/기초 수학 (AI)
벡터는 숫자를 원소로 가지는 1차원 배열.
행렬은 벡터를 원소로 가지는 2차원 배열이다.

x : 벡터, X : 벡터.

행렬의 특정 행(열)을 고정하면 행(열) 벡터라 부릅니다. (그림참고)
m개의 행과 n개의 열로 이루어져 있음.
몇 행의 행 벡터, 몇 열의 열 벡터.
유심히 보고 이해해라.
전치 행렬

전치 행렬은 n개의 행과 m개의 열로 이루어짐. 명확하게 이해할 부분.
벡터에 transpose하면 행벡터는 열벡터가 됨. 열벡터는 행벡터.
벡터는 공간에서 한 점, 행렬은 여러 점.
행렬의 행벡터 xi는 i번째 데이터를 의미한다.
행렬의 xij는 i번째 데이터의 j 번째 변수의 값을 말한다. (i번째 행의 j번째 값.)
벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다.
성분곱, 스칼라곱 또한 벡터와 같다.
행렬 곱셈

X, Y 행렬을 계산할 때 X의 열의 개수와 Y의 행의 개수가 일치하면 가능.
i 번째 행벡터와 j 번째 열벡터 사이의 내적으로 계산된 것.
행렬도 내적이 있을까?
numpy의 내적은 i 번째 행벡터와 j 번째 행벡터를 내적하는 것이기 때문에
수학에서의 개념과는 다르다!

X행렬과 Y전치행렬의 곱. X의 행벡터와 Y의 행벡터의 개수가 같아야 함.
행렬을 이해하는 방법
행렬은 벡터공간에 사용되는 연산자로 이해한다.
(다른 두 데이터를 연결하는 방법으로 이해)

A 행렬과 x 벡터의 곱 = z 벡터
z벡터와 x벡터를 A라는 행렬로 이어줄 수 있다.
이런 행렬 곱을 이용해서 벡터를 다른 차원으로 보내줄 수 있고,
주어진 데이터에서 패턴을 추출할 수 있고 압축을 할 수 있다. 기계 학습에서 매우 많이 사용. (선형 변환)
딥러닝은 선형 변환과 비선형 함수의 조합으로 이루어져 있음.
역행렬
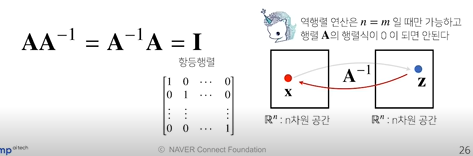
어떤 행렬의 연산을 거꾸로 되돌리는 행렬을 역행렬이라고 함.
역행렬은 행과 열 숫자가 같고 행렬식이 0이 아닌 경우에만 계산할 수 있음.
행렬은 순서가 민감하지만, 역행렬은 순서가 상관 없음.

역행렬을 구하는 함수를 이용할 수 있음. (행과 열을 개수가 같은지 체크)
행과 열의 개수가 다르면 역행렬을 구할 수 없음.
유사 역행렬 (sudo 역행렬, 무어-펜로즈 역행렬)

행과 열의 개수가 달라도 계산을 해볼 수도 있다.
행이 열보다 많은 경우와 열이 행보다 많은 경우에 따라서 계산하는 방식이 달라짐

행이 열보다 많다면 유사역행렬은 원래 행렬의 앞에서 곱해주어야 항등행렬이 나온다.
열이 행보다 많다면 유사역행렬은 원래 행렬의 뒤에서 곱해주면 항등행렬이 나온다.

연립방정식의 해를 구하기 위해서 식의 개수와 변수의 개수가 같아야 함.
변수의 개수가 식의 개수보다 많은 경우에는 식을 만족하는 변수의 개수가 많아지기 때문에 해가 무한히 많다. 부정이라고 배웠음.
유사역행렬은 그 중 하나의 해를 구하는 것이라고 볼 수 있다.

행렬과 벡터의 곱으로 표현
A 행렬 곱하기 x 행벡터는 b 열벡터
행렬 방정식을 풀 때 유사역행렬을 이용해서 해를 구할 수 있음

식의 개수보다 변수가 많은 경우이다. 무어-펜로즈 법칙으로 좌측에 A+를 곱해주게 되면 x라는 해를 구할 수 있다.
변수의 개수가 식의 개수보다 많은 경우에는 연립방정식 문제를 풀수가 있다.
선형회귀분석

변수의 개수보다 식의 개수가 더 많은 경우는 선형회귀분석의 문제일 경우가 많다.
이 경우에도 유사역행렬을 구할 수 있다.
선형 회귀 식(y)을 찾는 방정식. 어떤 베타를 써야 X행렬을 잘 표현할 수 있을까.
이때 선형회귀분석은 행(식)이 더 많기 때문에 방정식을 푸는 것은 불가능하다.

데이터를 최대한 잘 표현될 수 있는 선을 찾는 것이 최선이다.

두 사이의 거리를 최소화 한다.
선형 모델 식을 y의 해쉬로 표현.
실제 y의 값과의 차이를 최소화
y의 가장 근접한 값. (y와 유사y) L2 노름을 최소화할 수 있는 베타

y절편을 구해서 더해주어야 함.

'requirement fot AI > 기초 수학 (AI)' 카테고리의 다른 글
| 통계 : 다양한 분포들을 간단히 알아보자. (0) | 2022.01.02 |
|---|---|
| 4. 경사하강법 (Gradient Descent) (0) | 2021.12.08 |
| 통계 : p-value (0) | 2021.12.08 |
| 통계 : ABtest (0) | 2021.12.08 |
| 통계 : 의사결정나무 (0) | 2021.12.08 |