2021. 12. 8. 19:46ㆍrequirement fot AI/기초 수학 (AI)
변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d 차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡고 가자
미분
변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구이다. (최적화에서 제일 많이 사용하는 기법)
극한을 사용한다.

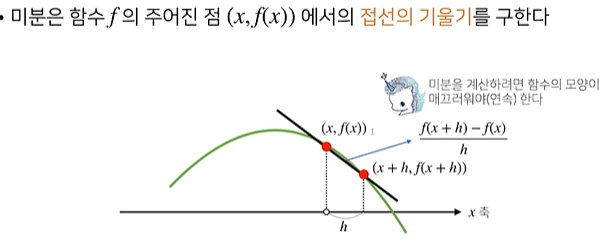
기울기를 계산할 때, 주어진 함수 와 이동시킨 함수를 이동량으로 나눠주면 기울기.
기울기를 변화율이라고 부름

파이썬 라이브러리에 미분을 할 수 있다.
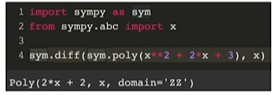
아래 함수에서 h를 0으로 보내주게 되면
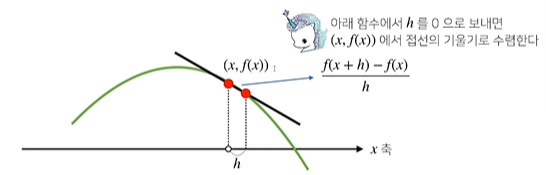
한 점에서의 접선의 기울기를 알 수 있다. 한 점에서의 접선의 기울기를 알 수 있다면,
어느 방향으로 점을 움직여야 함수 값을 증가, 감소 시킬지 알 수 있다.
미분 값을 더해주면 증가, 빼주면 감소.

미분값이 더해주면 (gradient ascent)
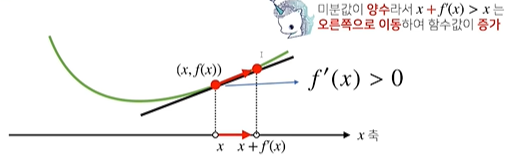
점은 미분값이 음수이든 양수이든 증가하는 방향으로 이동한다.
빼주면 감소하는 방향으로 이동함. (gradient descent)
경사 상승법은 극대값의 위치를 찾을 때 사용함.
경사 하각법은 함수의 극소값의 위치를 구할 때 사용함.
극 값에 도달하면 움직임을 멈춘다.

미분값이 0이 되기 때문이다.

컴퓨터는 미분을 해서 0을 거의 구할 수 없다. eps보다 작아지면 종료함.
학습률을 조정하면 경사하강법의 속도를 조절할 수 있음.
주어진 함수의 극소값을 찾아주게 됨.
다항함수 일때 경사하강법.

변수가 벡터인 다변수 함수일 경우 편미분을 사용한다.

x 방향의 편미분, y 방향의 편미분을 할 수 있다. 주어진 변수의 개수만큼 계산한 그레디언트 벡트를 이용하여 경사하강/상승법에 이용할 수 있다. 각 변수를 편미분한 벡터를 담은 것을 그레디언트 벡터라고 힌디/


-를 붙여주면 가장 빨리 감소하게 되는 방향과 같다. (-를 안 붙이면 증가하는 방향.)
임의의 차원의 함수의 최솟값, 최댓값을 구할 수 있다.

벡터이기 때문에 노름을 이용해야함.

다변수 함수에 대해 gradient descent를 적용하는 코드.
'requirement fot AI > 기초 수학 (AI)' 카테고리의 다른 글
| 통계 : 회귀 (0) | 2022.01.08 |
|---|---|
| 통계 : 다양한 분포들을 간단히 알아보자. (0) | 2022.01.02 |
| 3. 행렬 개념 정리 (0) | 2021.12.08 |
| 통계 : p-value (0) | 2021.12.08 |
| 통계 : ABtest (0) | 2021.12.08 |