2021. 12. 8. 07:56ㆍrequirement fot AI/기초 수학 (AI)
데이터의 차이를 확인하고 설명하기 위해서 조건부 확률, 조건부 평균을 구해야 함.
하지만 방법을 생각하는 건 참 어려움.
하지만 통계학자들이 도구를 만들어 두었다. 그중 하나가 의사결정나무.
의사결정나무를 보기전에 먼저 분할 정복을 알아야 한다.
분할 정복이란 데이터를 여러 개의 부분으로 쪼개고, 나뉜 부분별로 분석을하는 방법.
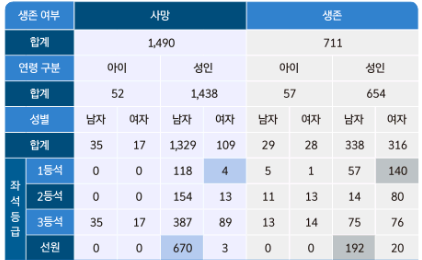
총 2201명이 타고 있었고 711명만 살아남았다. 또한 성별, 좌석 등급, 연령 구분에 따라 분할되어 있음.
조건에 따른 사망자 수, 생존 수를 파악할 수 있다. 예를 들어 성인, 여자, 1등석, 생존자의 수는 140명이고, 사망자 수는 4명이다. 또한 성인, 남자, 선원의 생존자 수는 192명이고, 사망자 수는 670명이다.
숫자로 파악하는 것은 어렵기 때문에 그림으로 표현해보자.

위 그래프는 범주형 변수가 만들어 내는 그룹의 크기에 따라 사각형으로 표현하는 모자이크 그림.
좌석 등급으로 먼저 표현되었다. 넓이의 폭은 좌석에 따라 타고 있는 사람의 수임. 3등석과 선원이 굉장히 많음.

높이를 가로로 또 나누어보자. 총 사각형의 개수는 8개, 좌석에 따른 성별의 비율이 보이기 시작한다.

폭을 세로로 나누어 아이를 또 표현했다. 선원에 아이는 없기 때문에 선으로 표현. 이 것을 포함하면 16개의 사각형이 만들어짐.

세로를 가로로 나누어 생존과 사망을 표현해보자. 회색과 파란색의 상자를 묶어서 16개의 사각형, 즉
16개의 그룹에 대해 한 눈에 생존과 사망의 비율을 볼 수 있다. 여자와 아이들의 생존자의 수가 높고, 좌성 등급이 높은 사람들의 생존율이 높은 것을 확인할 수 있다.
하지만 이 것이 최선일까? 3등석의 그룹들을 살펴보면 여자 승객의 아이와 성인의 생존율이 차이가 나지 않는다.
이렇게 나눠진 그룹의 차이가 크게 없다면 굳이 나눌 필요가 없다.
이 때 이 두 그룹의 차이를 명확하게 볼 수 있는 방법이 의사결정나무
의사 결정 나무
큰 차이도 없는 조건들까지 다 살펴보면 무의미한 일. 즉 세 개의 설명 변수로 조합 가능한 16개의 그룹을 모두 살펴볼 필요는 없다.
통계학자는 모든 설명 변수가 아니라 중요한 변수를 선택해서 차이를 설명하는 통계 모형을 만들었다.
의사결정나무는 그 중에서도 직관적으로 이해할 수 있는 모형이다!
의사 결정 나무는 전체 관측 치를 둘로 나눌 최적의 변수를 찾음. 차이를 설명하고 싶은 우리는 변수로 나누어진 두 그룹의 차이가 클 수록 좋음.

예를 들어 한 초등학교의 안경을 쓴 사람의 비율이 30퍼센트라고 해보자.
고학년과 저학년을 나눠 안경을 쓴 학생의 비율을 살펴보니, 31퍼센트, 29퍼센트로 측정 되었다.
또 남성과 여성으로 나누어 안경잽이 비율을 살펴보니, 40퍼센트, 20퍼센트로 측정 되었다.
'학년'과 ' 성별' 두 변수중 '안경 쓸 확률'을 더 잘 설명한 것은 성별이다! 의사 결정 나무는 이렇게 그룹끼리 더 큰 차이를 만드는 변수를 찾아준다!
타이타닉 호 데이터로 한번 알아보자.
나무의 몸통 -> 전체 관측치가 다 모여있습니다. 2201명 중에 711명이 생존했으므로 생존율은 32퍼센트.
의사 결정 나무 모형은 최적을 조건을 찾는다.

남자일 경우 생존율 21퍼센트, 여자의 경우 73퍼센트 (성별이 가장 큰 차이를 보이기 때문에 선택됨.)

가지를 더 뻗어줌. 여자일 경우 좌석등급의 3등석일 경우 생존율 (3등석일 경우 46퍼센트, 나머지 등급일 경우 93퍼센트)

남성의 경우, 어른일 경우 생존률은 20퍼센트, 어른이 아닐 경우 좌석등급이 3등석일 경우 생존율은 27퍼센트이고 3등석이 아닐 경우 전부 생존했다.
자 이제 왼쪽 남성, 성인의 생존율은 20로 가장 낮다. 이 이후로 의사결정나무는 가지를 더 뻗지 않았다.
의사결정나무가 이 이상은 큰 차이가 없을 것이라고 판단한 것.
남자 어른의 생존율은 20퍼센트 그리고 남자 아이가 3등석이 아닐 경우 생존율은 100퍼센트인 것을 알게 되었고,
여성이 3등석이 아닐 경우에는 93퍼센트의 생존율을 가지게 된것으로 매우 높은 것을 알게 되었다.
이렇게 모든 그룹을 보지 않아도 의미 있는 차이를 보여주는 5개의 그룹만으로 효율적으로 생존율의 차이를 보여주었음.
우리는 범주형 변수인 조건부 확률 (생존, 죽음)을 구했음. 만일 관심 변수가 연속형 변수라면 조건부 평균을 계산하게 됨.
'requirement fot AI > 기초 수학 (AI)' 카테고리의 다른 글
| 통계 : p-value (0) | 2021.12.08 |
|---|---|
| 통계 : ABtest (0) | 2021.12.08 |
| 통계 : 심슨의 역설 (0) | 2021.12.08 |
| 2. 벡터 개념 정리 (0) | 2021.12.02 |
| 1. 딥러닝 기본 용어 설명 (0) | 2021.12.01 |