2021. 12. 8. 12:07ㆍrequirement fot AI/기초 수학 (AI)
우리는 전의 글에서 살충제에 따른 죽은 벌레의 수에 대한 정보량을 얻는 방법을 알아보았다.
살충제와 죽은 벌레의 수의 관련성은 분산의 정보량 (그룹차와 개인차)으로 어느정도 파악할 수 있다.
하지만 그 정보량이 얼마나 커야 충분할까(의미가 있을까)? 그것을 지금부터 알아보도록 하자.
충분히 큰지 아닌지를 판단하기 위해서는 기준이 필요하다. 통계에서는 그래서 표본이라는 개념을 활용.
수억 개의 모래알에서 모래를 한 줌 퍼올린다고 상상하자.
통계에서는 이 수 억개의 모래알을 모집단이라고 하고, 손에 쥔 모래가 표본이라고 비유할 수 있다.
어떤 올림픽에서 특정 색의 메달을 얻을 확률, 살충제의 효과를 우린 얻을 수 있었다.
하지만 우연인지 운명인지 어떻게 판단할 수 있을까.
모집단에서 여러 표본을 가져와서 비교해본다!
예를 들어 내가 아주 고운 모래를 구했다고 치자. 그런데 친구가 그냥 해변의 모래와 다르지 않다고 주장한다.
이 것을 해결하는 방법은 간단하다. 내가 가진 모래의 평균 굵기를 계산하고, 친구가 해변의 모래를 가져와 평균 굵기를 계산해서 비교해보면 된다. 하지만 내 모래와 해변의 모래를 여러번 비교를 하는 것은 힘들다.
그래서 통계학자들은 조금 다른 접근 방법을 만들었다. 바로 표본(친구가 해변에 가져온 모래 한 줌)들의 평균 모래 굵기들의 패턴을 찾는 것이다.
내 모래알의 평균 굵기는 3이고 친구가 10번이나 가져온 모래 한 줌의 평균 굵기는 아래와 같다.

이를 히스토그램으로 표현하면

친구가 승복을 하지 않고 더 가져오게 된다면,

이고,

의 히스토그램으로 표현할 수 있다.
역시 내 모래보다 고운 모래를 찾을 수 없었다. 만일 친구가 1000개의 표면을 더 가져오면 히스토그램은 어떻게 될까

대략 평균은 5에 가까워보이고, 5 근처의 값들이 많다는 점과 모양이 좌우대칭인 것을 알 수 있다.
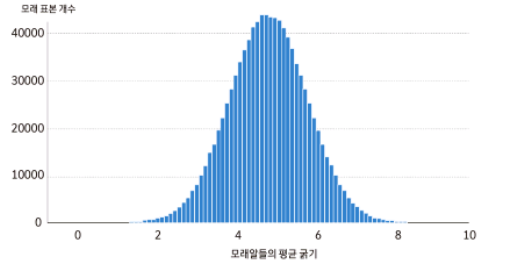
100만개의 표본을 가져오고 평균 굵기를 더 세분화(0.1 간격)해서 히스토그램을 그렸다.
이렇게 데이터로부터 계산된 통계량의 패턴을 분포라고 한다.

우리 모래의 평균이 3이다. 그러니 해변에서 가져온 모래의 약 상위 1~2퍼센트에 들 정도이니
해변에서 가져온 모래에 비해 훨씬 곱다. 라는 분석을 할 수 있다.
우리는 연속형 변수가 어떤 관계를 가지고 있는지 살펴볼 때 상관관계를 계산을 한다.
-1 부터 1 사이의 값을 가지는 이 수는 양의 상관 관계, 음의 상관 관계, 관련이 없는 지를 알려준다.
서로 전혀 상관이 없는 변수를 비교하면 0에 가까운 값이 나올 것이다.
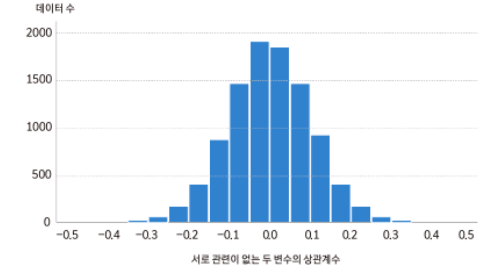
관련이 없는 두 변수를 10000개를 서로 상관관계를 비교한 것. 그 중심에 0이 있는 것으로 상관관계의 평균은 0이라고 짐작할 수 있다.
상관관계의 절대값이 0.3이 넘는 데이터는 22개가 있다. 통계에서는 0.22퍼센트로 일어날 수 있는 확률로 본다.
(0.0022 * 100)
아빠와 아들키가 상관관계가 0.5라고 가정하자. '아무 관련이 없는 변수의 상관관계' 에서는 거의 나오지 않는 숫자이다.
그러니 우리는 아빠와 아들키의 상관관계 0.5는 아무 관련이 없다고 보기 힘들며 굉장히 의미가 있는 숫자라고 볼 수 있음.
두 범주형 변수의 관계는 AB테스트로 계산한다!

두 가지 배너를 보여주고 어떤 배너가 매력적(배너를 보고 클릭을 했는지, 아닌지)인지 이용자 100을 대상으로 설문함.
100명의 사람에게 각 그룹은 50번씩 동등하게 노출되었고, 배너A가 35번의 높은 반응 보였다.
그렇다면 우리는 A의 반응이 더 좋은 것이 '우연'이 아닐까?
또다시 비교를 해야한다.
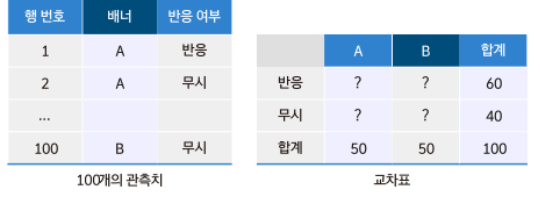
두 변수의 값 100개가 어떻게 채워지는가에 따라 교차표의 네 칸은 달라지겠지만, 행 합계와 열 합계, 그리고 전체 합계는 각 조건이 정해져 있다. 어떤 값으로 표를 채우든 상관없이 배너 A와 배너 B의 반응률을 계산할 수 있다.

배너 a를 알면 나머지도 전부 계산할 수 있다. 만일 배너에 따라 반응률이 차이가 없다. (그룹에 따른 차이가 없다.)
로 가정을 한다면 배너 A와 B가 각각 30에 가까운 평균 값을 가질 것으로 예상할 수 있다. 1000개의 랜덤 샘플을 만들고 히스토그램을 만들어보자.
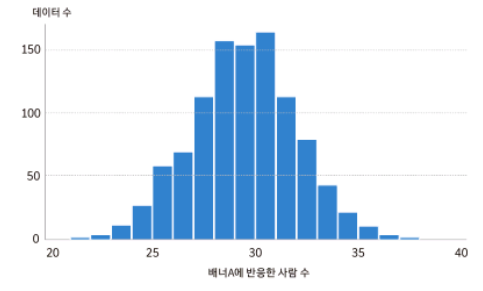
그룹에 따라 반응률이 차이가 없다라는 것을 가정한 랜덤 샘플의 a 값의 분포이다. 역시 30을 중심으로 분포가되어 있음.
35보다 큰 값이 나온 표본은 1000개 중 단 39개이다. 반응률과 배너가 관련이 없다는 가정하에서 100명 중 39명이 반응할 확률은 3.9퍼센트인 것이다. 하지만 우리 눈앞에 이 3.9퍼센트의 확률로 나올 데이터가 나왔으니 충분히 의미가 있을 수 있다라고 봐야한다.
지금까지 데이터가 가진 차이의 의미를 설명하기 위해서 분포의 힘을 빌렸다.
차이가 없는 상황을 가정하고, 우리가 가지고 있는 데이터와 모양새만 똑같은 랜덤 샘픔들로 분포를 만들어 냈다.
그리고 단 하나밖에 없는 실제 데이터의 값을 집어넣고 상대적인 위치를 확률로 계산하였다.
이 확률 값을 우리는 p 값이라고 한다. p 값을 계산하는 목적은 우리의 데이터 속 차이가 얼마나 의미가 있는지를 확인하기 위해서이다. 그룹에 따른 차이가 없다는 가정하에 pvalue가 0에 가까울 수록 실현 불가능한 만큼 큰 차이를 보인다는 것을 의미하고, 커질수록 우연히 일어날 수 있는 흔한 차이를 의미한다.
그렇다면 도대체 p 값은 얼마나 작아야 할까? 차이의 의미가 있다, 없다를 판단하는 기준값은 있을까?
이는 다음 시간에!
'requirement fot AI > 기초 수학 (AI)' 카테고리의 다른 글
| 4. 경사하강법 (Gradient Descent) (0) | 2021.12.08 |
|---|---|
| 3. 행렬 개념 정리 (0) | 2021.12.08 |
| 통계 : ABtest (0) | 2021.12.08 |
| 통계 : 의사결정나무 (0) | 2021.12.08 |
| 통계 : 심슨의 역설 (0) | 2021.12.08 |