2021. 11. 13. 04:29ㆍ파이썬/알고리즘
첫 줄 :
배열의 길이 : N
더하는 횟수 : M
연속으로 같은 값의 수 : K
두번째 줄 :
숫자 배열이 온다.
위의 규칙을 따르는 가장 큰 수를 구하시오.
input :
5 8 3
2 4 5 4 6
output:
46
가장 큰 수가 k번 나오면 두 번째로 큰 수가 나오면 됨. 이 것을 m번 반복.
n,m,k = map(int, input().split())
num_list = list(map(int, input().split()))
num_list.sort()
print(num_list)
total = 0
temp = k
for count in range(m) :
if k != 0 :
total += num_list[-1]
print(num_list[-1])
k -= 1
elif k == 0:
total += num_list[-2]
print(num_list[-2])
k = temp
print(total)생각보다는 쉬운 문제

똑똑하게 푸는 법
반복되는 수열에 대해서 파악. 가장 큰 수와 두 번째 큰 수가 더해질 때 일정하게 반복해서 더해지는 특징이 있음.
반복되는 수열의 길이는 바로 k+1, 따라서 M을 k+1 나누면 수열이 반복되는 횟수가 됨. 다시 여기에 k를 곱해주면 최댓값의 빈도를 구할 수 있음. 이때 k가 나눠지지 않을 때의 경우를 더해주어야 함. M을 (k+1)로 나눈 나머지!
그렇다면 int(M / (K+1)) * k + M % (K+1)이 가장 큰 횟수가 됨. 두 번째로 큰 수가 등장하는 횟수는 M에서 최댓값의 빈도만큼 빼주면 된다.
최댓값의 빈도를 구한다!
그러면 자연스럽게 두 번째로 큰 수가 나온다.
수열의 규칙을 찾으면 빈도 수를 구할 수 있다.
위 문제와 같은 조건일 경우,
[6,6,6,5,6,6,6,5]가 된다.
[6,6,6,5]가 2번 반복됨. 즉 k+1이 하나의 최소 반복이 되는 길이가 됨. m을 k+1로 나누면 2가 됨.
그리고 이 안의 최댓값의 갯수는 k개이다.
추가로 안 나눠질 경우엔 나머지를 더해주면 됨
그러므로
(m//k+1) * k + (m%(k+1))
import time
n,m,k = map(int, input().split())
num_list = list(map(int, input().split()))
# 최대값의 등장 횟수 (m//k+1) * k + (m%(k+1))
start_time = time.time()
num_list.sort()
max_freq = int(m/(k+1) * k + (m % (k+1)))
prev_max_freq = m - max_freq
value_1 = max_freq * num_list[-1]
value_2 = prev_max_freq * num_list[-2]
big_sum = value_1 + value_2
end_time = time.time()
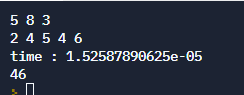
print(f"time : {end_time - start_time}")
print(big_sum)
'파이썬 > 알고리즘' 카테고리의 다른 글
| 6. 구현 : 상하좌우 움직이기 (0) | 2021.11.13 |
|---|---|
| 5. 구현 : 문제 풀이 전략 (0) | 2021.11.13 |
| 4. 그리디 알고리즘 : 1이 될 때 까지 (0) | 2021.11.13 |
| 3. 그리디 알고리즘 : 카드 게임 (0) | 2021.11.13 |
| 1. 그리디 알고리즘 : 그리디 알고리즘 소개, 최소 거스름돈 동전 개수 문제 (0) | 2021.11.13 |